Image Warping and Mosaicing (Part 1)

Aaron Zheng

Overview

In this project, we will be adding on to the image warping of the previous project, and we will be discovering how to put two images that are a perspective transform of each other together in such ways as to form a mosaic, or a panoramic view. First, we have to find the homography that best suits the two pairs of images, and then we will warp one image into the other's perspective, and combine them in intelligent ways.

Shoot the Pictures

For this project, I took many different pictures of places, including on the street next to my apartment, in Berkeley, and in tourist places. The 3 pairs of images that I will be showing are images that turned out pretty well. In the end of the page, I also include some pairs of images that did not turn out so well.

The left image will be known as image A, and the right is image B.

Recover Homographies

For this step, I defined point correspondences between the pairs of perspective transformed images, and using these I was able to derive a solution for the homography. A big problem I faced here was the great inaccuracy of using a direct least squares solution... directly using least squares was very unstable and always had errors of high magnitude.

So instead, I solved the expression by summarizing each point correspondence into two linear equations, putting them as rows into a matrix A, and taking the SVD of A. Then, the least squares problem just becomes the smallest eigenvector of A.

The left image is point correspondences on image A, and the right image is point correspondences on image B.

Warp the Images

Here, I warped the images using the homographies defined above. It involved using the homography, expressed as a matrix, and multiply it by the image matrix. We define image A and image B, and one homography will convert image A to B. Likewise, the reverse homography will convert image B to A.

To make this work properly, I used the griddata function from scipy and took the coordinates of the corners of each image and applied it to the homography. This got me the "bounding shape" of the transformed image. Then, I create a new image frame which fits this "bounding shape", and transform the image into the shape. This way, no information is lost.

The left image is image A transformed into the perspective of image B, and the right image is vice versa.

Image Rectification

Image rectification (making perspective transformed rectangles look like regular rectangles using homographies) is an interesting use case of image warping. Here, I rectified some images:

Rectification Building

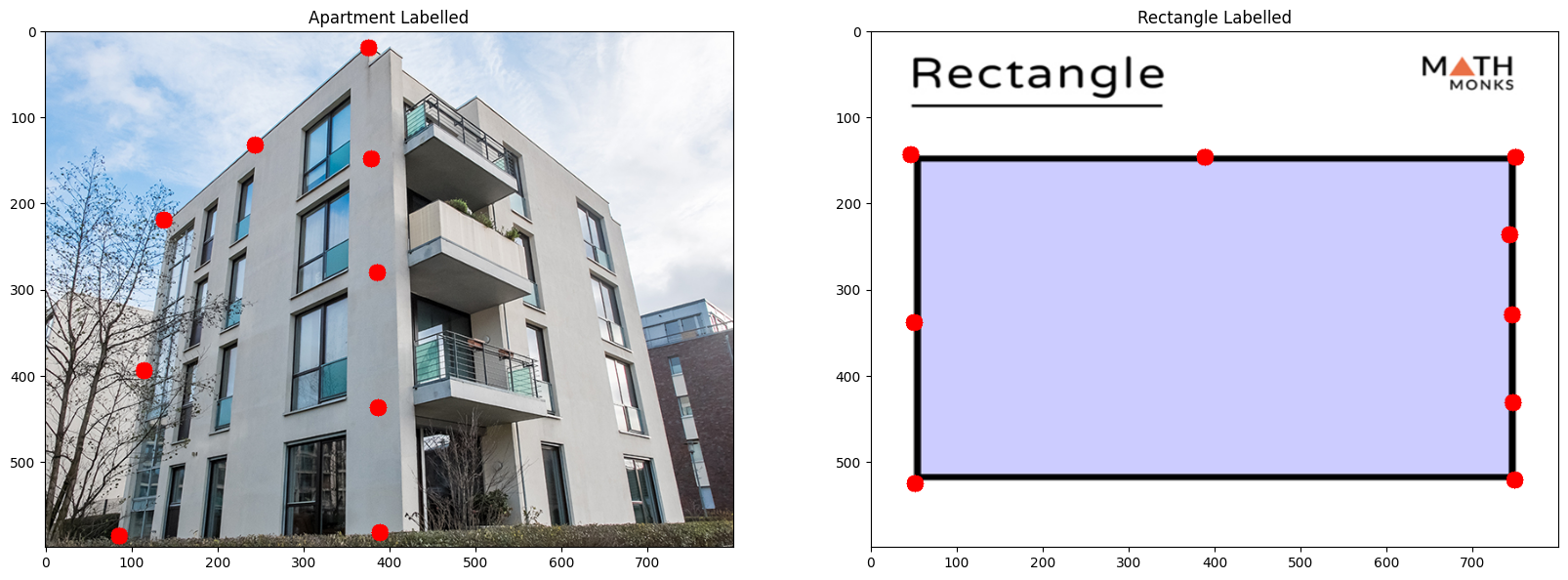
Rectificied Result

Rectification Generic

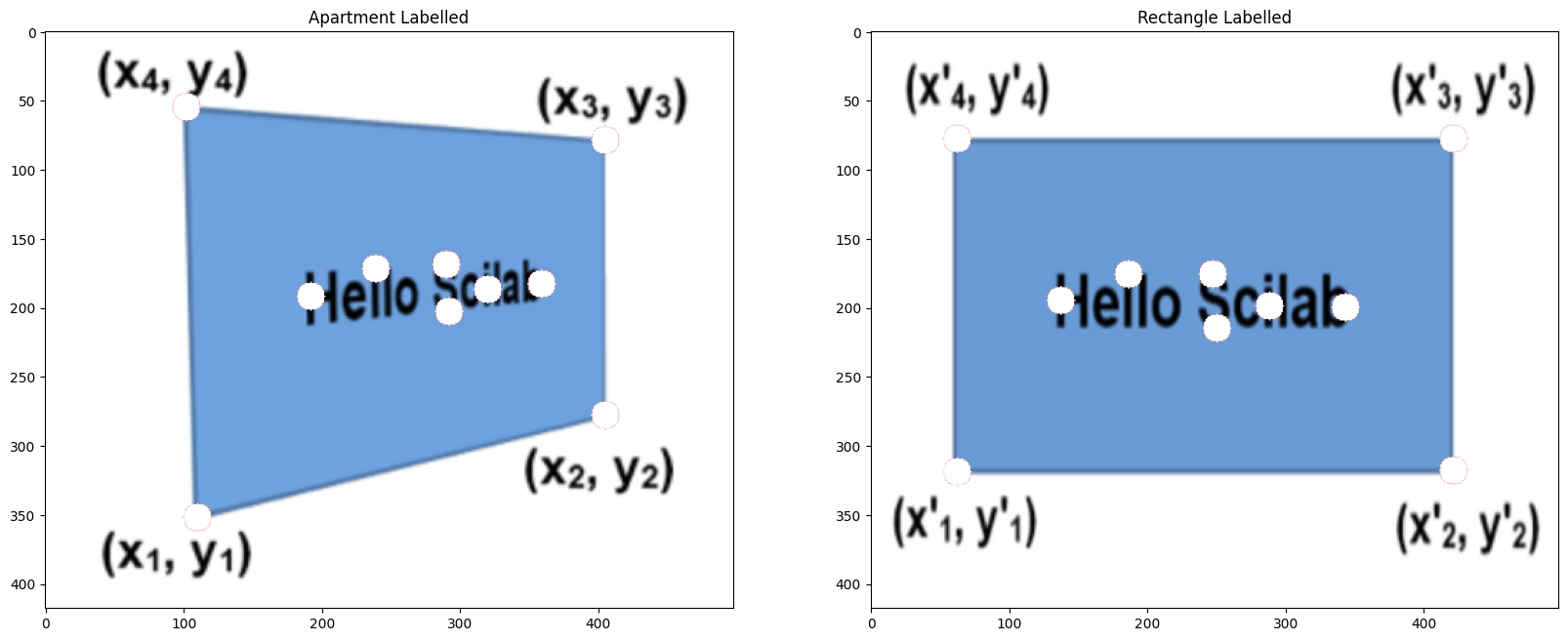
Rectificied Result

Rectification (My Ipad)

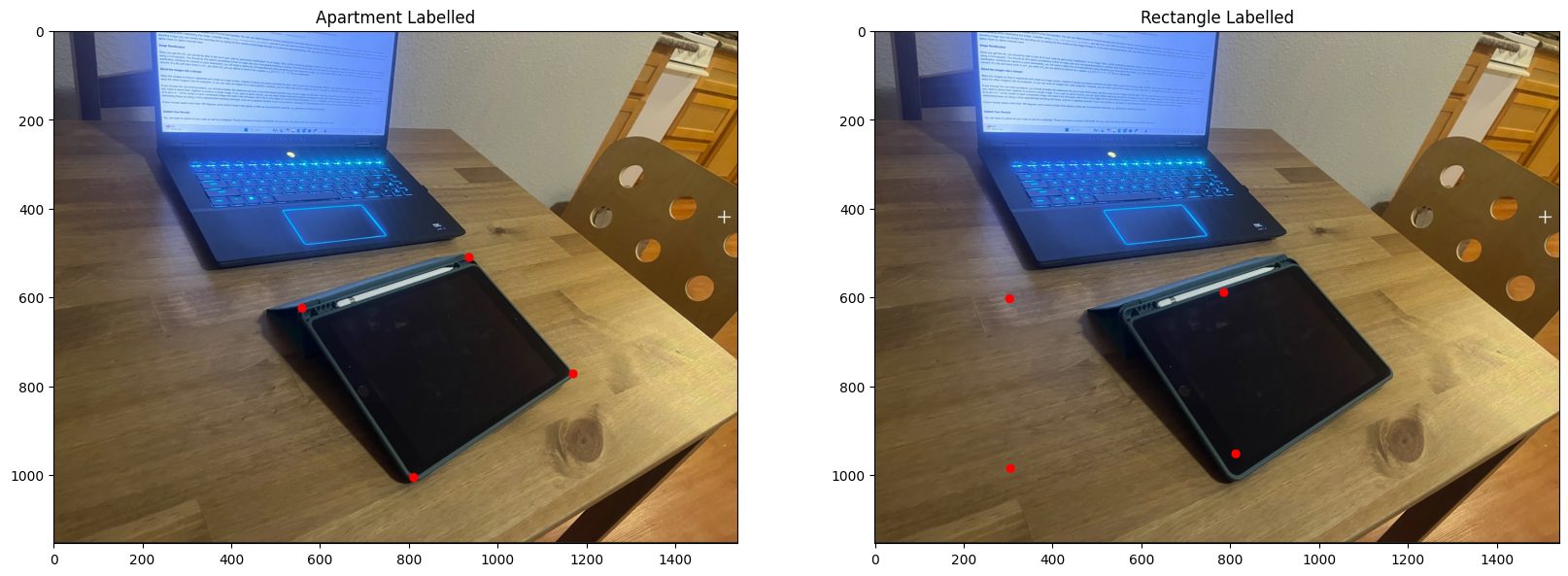
Rectificied Result

Mosaic'ed Image

To blend images, I left one image unwarped, and the other warped. Then I transformed either one or both of the warped and unwarped images, in such a way that they fit nicely together. Then I added the two images together.

Using the alpha masks I created for both the warped and unwarped images, I was also able to do a laplacian blending of the two images, although this didn't turn out perfectly.

Failed Images

Below is an example of a failed image pair. This is one of the first images I took. The reason the mosaic of this image failed is because the perspective transform angle is too great.

Below are the original image A and B

Below is the attempted image warping of A and B

Since the warping magnitude is so great, it is clear that this image pair cannot make a good mosaic.

Conclusion

This was a fun project, I very much enjoyed it. I learnt (and struggled) a lot, especially when it came to making the homography work, and combining the warped and unwarped images.